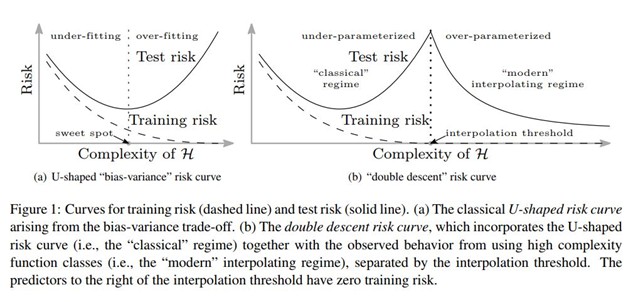
La parte sinistra della figura precedente mostra una delle curve più famose che si possono incontrare nell’apprendimento automatico. Rappresenta il cosiddetto “compromesso bias varianza”.
Accadono diverse cose. Cominciamo con l’asse delle ascisse: i valori più bassi corrispondono a modelli con una minore complessità, con pochi parametri, mentre i valori più alti implicano modelli più complessi, con un gran numero di parametri. Sull’asse delle ordinate è indicato il rischio che il modello commetta errori sia in fase di addestramento che di test.
L’asse delle ascisse talvolta viene denominato “capacità della classe di ipotesi” e questa dicitura corrisponde al concetto di complessità di un modello e al numero dei suoi parametri. Il numero di parametri regolabili in un modello determina l’insieme ipotetico di funzioni che possono essere implementate utilizzando quel modello. In sostanza siamo limitati a trovare una soluzione da tale insieme.
Supponiamo di volere un modello lineare, ad esempio una semplice retta che interpoli una serie di dati rappresentati da coordinate sparse su un piano cartesiano. Questa retta è definita dalla sua pendenza e dal suo spostamento rispetto alle origine: abbiamo quindi bisogno di due parametri. Ma se il modello disponesse di un solo parametro? Allora saremo costretti a trovare una funzione più semplice, in cui la pendenza sia fissa o lo spostamento sia fisso, limitando così le nostre opzioni.
In un modello non lineare maggiore è il numero di parametri, minore è il numero di funzioni che abbiamo a disposizione, quindi il numero di parametri è una misura della complessità del modello e determina l’insieme delle funzioni a cui si può attingere per trovare una buona soluzione. Questo insieme può anche essere chiamato “classe di ipotesi”. All’aumentare del numero di parametri aumenta la capacità della classe di ipotesi.
Torniamo alla curva di cui sopra. Si vede una curva tratteggiata. Inizia con un valore alto sull’asse delle ordinate per i modelli più semplici e tende a zero all’aumentare della complessità del modello. Questa curva rappresenta il “rischio di addestramento”, ovvero il rischio che il modello commetta errori sul set di dati di training. E chiaro che i modelli estremamente semplici si comportano male sul dataset di addestramento, dato che si adattano poco ai dati, ed è altrettanto chiaro che quando i modelli diventano più complessi iniziano ad adattarsi meglio e il rischio di addestramento tende a zero.
La curva continua rappresenta invece il rischio di errore durante il test inizia con un valore alto sull’asse delle ordinate per i modelli a bassa complessità, scende fino a un minimo e poi ricomincia a salire. Il “fondo della scodella” e dove vogliamo che si trovi il nostro modello di ML: quel punto rappresenta l’equilibrio ottimale tra i cosiddetti underfitting e overfitting, ovvero tra un modello sottodimensionato ed uno sovradimensionato, tra la semplicità e la complessità del modello. Qualcuno l’ha chiamata la zona “Riccioli d’oro” (Goldilocks). La scelta di un modello che riduce al minimo il rischio di errore nei test massimizza la capacità del modello di generalizzare i dati non ancora visti, ovvero i dati che il modello incontrerà in natura, per così dire, in quanto non fanno parte né dei dati di addestramento né di quelli di test. Quindi, minimizzare l’errore di test implica minimizzare l’errore di generalizzazione, ovvero massimizzare la capacità di generalizzare.
Da quasi tutti i risultati empirici sull’addestramento tradizionale, questa storia sembrava corrispondere al vero. Ma poi le reti neurali profonde sono entrate nella mischia e hanno ribaltato questa saggezza convenzionale. Le reti profonde hanno in teoria troppi parametri rispetto alle istanze dei dati di addestramento si dice che esse sono iper-parametrizzate (ad oggi se ne conoscono, quelle dietro agli LLM, anche con cinquecentomila miliardi di parametri). Dovrebbero quindi adattarsi troppo e non generalizzare bene i dati di prova non ancora visti. E invece lo fanno! La teoria standard del ML non è in grado di spiegare in modo adeguato perché le reti neurali profonde funzionano così bene.
Adesso si faccia riferimento alla parte destra dell’immagine sopra. La pratica dell’utilizzo delle reti neurali profonde e la sperimentazione hanno portato a scoprire, contrariamente a quanto ci si aspettava, che aumentando il numero di neuroni, e quindi la capacità del modello, la rete non si adattava eccessivamente ai dati di addestramento. In un primo momento, aumentando le dimensioni della rete sia l’errore di addestramento che quello di test diminuivano come previsto. Mamma mano che la rete aumentava ulteriormente le dimensioni e l’errore di addestramento si avvicinava zero, come nella curva a sinistra, l’errore di test (o errore di generalizzazione) avrebbe dovuto incominciare ad aumentare. Ma non fu così. Le parole del documento originale della ricerca, del 2015, riflettono l’incredulità dei ricercatori.
«Ancora più sorprendente il fatto che se si aumenta la dimensione della rete oltre quella necessaria per ottenere un errore di addestramento pari a zero, l’errore di test continua a diminuire! Questo comportamento non è affatto previsto dalla teoria, anzi è proprio l’opposto rispetto a quello che ci si attende se consideriamo l’apprendimento come rispondente a una classe di ipotesi influenzata dalla dimensione della rete. Quando si aumenta la complessità la rete non si adatta meglio ai dati di addestramento… tuttavia, l’errore di test diminuisce. Infatti, aggiungendo sempre più parametri, anche oltre il numero di campioni di addestramento, l’errore di generalizzazione non aumenta.»
Un altro aspetto straordinario e del tutto inatteso fu lo scoprire che, introducendo deliberatamente del rumore nel set di dati, la rete in qualche modo lo accoglieva in sé.
Immaginate di avere a che fare con una rete neurale costruita per riconoscere immagini di numeri scritti a mano (in realtà questo è un modello di rete neurale molto famoso nel settore). Ogni immagine ha un’etichetta associata: “cinque” per il numero 5, “nove” per il 9 e così via. Prendiamo l’1% di queste immagini e rimescoliamo casualmente le loro etichette così, un’istanza del numero 5 potrebbe essere etichettata erroneamente come “quattro”, un’istanza del numero 8 come “uno” ecc. Poi dividiamo il dataset in dati di addestramento e dati di test, e addestriamo la rete neurale fino a raggiungere un errore pari a zero sui dati di addestramento. Che cosa sta succedendo mentre procediamo? Poiché abbiamo introdotto intenzionalmente del rumore nei dati, la rete, che non commette errori sui dati di addestramento, sta accogliendo in sé il rumore. Per esempio, sta imparando a riconoscere i numeri 5 e 9 etichettati, erroneamente come “quattro” e “due”. Ovvero si adatta perfettamente ai dati. La teoria dell’apprendimento ha un termine particolarmente evocativo per descrivere un modello che si comporta così: si dice che quest’ultimo frantuma i dati di addestramento.
Poiché si adatta perfettamente ai dati di addestramento contenenti rumore, questo modello non dovrebbe funzionare bene sui dati di test. La curva a ghirigori (pensate ad una curva che si adatti perfettamente, seguendoli fedelmente, ad una serie di punti sparsi in maniera casuale sul piano cartesiano), che il modello ha appreso è molto specifica per il rumore e ha rilevato e non c’è motivo di aspettarsi che il modello riesca a generalizzare. Ma non è quello che accade.
I ricercatori scoprirono che persino con il 5% di etichette casuali non c’è un overfitting significativo e l’errore di test continua a diminuire man mano che la dimensione della rete supera quella necessaria per ottenere un errore di addestramento pari a zero. Una vera e propria sfida concettuale alla teoria dell’apprendimento statistico, in quanto la misura tradizionale della complessità di un modello fatica a spiegare la capacità di generalizzazione delle reti neurali artificiali di grandi dimensioni. Ad oggi le reti neurali anche estremamente complesse riescono a interpolare molto bene i dati di addestramento e al tempo stesso fanno previsioni accurate sui dati di test, Essendo inoltre in grado di interpolare dati rumorosi, senza che l’accuratezza della previsione ne risenta, come invece ci si aspetterebbe.
Uno dei principi generali da sempre largamente condiviso, e che viene insegnato, è che non si vuole ottenere un adattamento troppo buono ai dati, altrimenti si avrà una scarsa accuratezza predittiva: ma quanto viene fatto continuamente nelle reti neurali profonde è esattamente l’opposto, e funziona stranamente bene. Durante un convegno recente sul deep learning uno dei massimi esperti affermò che Il modo migliore per risolvere il problema da un punto di vista pratico e costruire un sistema molto grande. Fondamentalmente si vuole essere sicuri di raggiungere un errore di addestramento nullo. Un’affermazione che andava contro la teoria dell’apprendimento standard ma i fatti dimostravano che la teoria standard non era adeguata in tutte le situazioni. Le reti neurali fortemente parametrizzate non si adattano eccessivamente ai dati, ovvero funzionano bene anche per i test. E la complessità, o capacità, dei modelli è sufficiente per interpolare dati rumorosi persino quando questo riguardava circa il 5% del dataset, le prestazioni delle macchine delle reti neurali non peggioravano come previsto.
La teoria va rivista.
Tutto questo ha portato a realizzare reti in grado di auto-addestrarsi che, senza il vincolo di dover etichettare i dati per l’apprendimento supervisionato, stanno diventando sempre più estese. Man mano che queste reti aumentano di dimensione, il loro comportamento sfida sempre di più la nostra comprensione tradizionale dell’apprendimento automatico.
La parte della curva in cui vi è la prima discesa della successiva salita è stata capita molto bene: la matematica ci spiega in modo dettagliato il comportamento dei sistemi di ML in questo regime sotto-parametrizzato. Ma il regime più recente, iper-parametrizzato, Che si traduce nella seconda discesa, è a malapena comprensibile da un punto di vista matematico. Si aprono territori inesplorati di cui, fortunatamente, perlomeno si dispone di una mappa.
Nonostante si sia continuamente evidenziato, come fa correttamente l’Autore, Il fatto che l’apprendimento automatico tradizionale ha sempre avuto alla base dei principi matematici ben compresi, le reti neurali profonde hanno rovesciato la situazione. Improvvisamente, le osservazioni empiriche su queste reti hanno preso il sopravvento sembra essere alle porte di un nuovo modo di fare AI.
Nessuno sostiene che quanto fanno le attuali reti neurali profonde sia ragionare, nonostante il considerevole dibattito, né che queste siano in grado di portarci dal riconoscimento di modelli basati sul ML a una vera AI in grado, effettivamente, di farlo; ma la strada verso questi territori inesplorati, è stata aperta. E che si sia in presenza di un comportamento emergente è certo: modelli la cui unica diversità è nella loro complessità e che condividono sostanzialmente la stessa matematica passano dal fallimento al successo nell’esecuzione di un compito loro assegnato. Non è magia né mistero, è solo un comportamento osservato che emerge in modo molto graduale e se qualcosa viene imparato è esclusivamente dovuto al fatto che la matematica sottostante lo permette.
Nel giugno del 2002 Google annunciò un linguaggio molto esteso chiamato “Minerva”, addestrato su 780 miliardi di parole prese da Internet. Fu addestrato a prevedere, in un certo senso, per inferenza, la parola mancante in una serie costituenti una frase. Il procedere degli LLM insomma: non fu addestrato per risolvere problemi matematici e men che mai a ragionare esplicitamente.
Quando a Minerva venne posta questa domanda ecco cosa accadde…

Minerva fu il primo LLM a rispondere correttamente al 50% delle domande tratte da un dataset chiamato MATH e contenente 12.500 domande di matematica della scuola superiore. Sembra proprio una risposta ragionata. Ma Minerva invece prende la domanda e la trasforma in una sequenza di oggetti (ad esempio parole), e predice ciò che seguirà, oggetto dopo oggetto.
Minerva produce semplicemente un testo basato su correlazioni nei dati di addestramento, non sta ragionando. Checché se ne dica da parte dei non addetti ai lavori.
Però secondo alcuni specialisti, le AI allo stato dell’arte non sono in grado di combinare la comprensione del testo con l’analisi logica; altri esperti di AI, invece, citano le risposte di Minerva alle domande matematiche e sostengono che fa esattamente questo: comprende il testo e ragiona sulla risposta. Molti la considerano solo una glorificazione di una complessa, non ben compresa, corrispondenza di schemi. La teoria di cui disponiamo non è abbastanza sofisticata da risolvere il dibattito gli esperimenti stessi non corroborano le affermazioni in un senso o nell’altro, ma forniscono semplicemente delle evidenze che devono ancora essere spiegate. Possiamo solo intuire cosa ci aspetta, quando le reti neurali estremamente estese incominceranno a ragionare, se non lo stanno già facendo: saremo davvero degli stranieri di un territorio sconosciuto.
Ma è scienza, non fantascienza.

